4 Matemaatika lähtetest
4.1 Üks ülesanne õpilase kohta
4.1.1 Test: 1. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Nimeta üks andmete kogumise meetod!
Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on maksimum?
2. taseme ülesanne: Esita näide mediaani kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite mood?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on sektordiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on elamumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida veerand arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Avaldist \(2x+3y-3x-5y\) nimetatakse\(2x+3y-3x-5y=\blank{-}x-2{y}.\)
Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[3x^2(\] \[xy-4y+5)=-36x^3y-\]\[x^2y+15x^2.\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: \(\begin{cases} 3x-4y=15\\ 2x-4y=-10 \end{cases} \rightarrow\)Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.13 on kahe funktsiooni graafikud. Sinine graafik esindab funktsiooni Oranž graafik esindab funktsiooniÕpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Võrdhaarses kolmnurgas \(ABC\) on \(DE \parallel AB\), \(CD=\qty{6}{\centi\m}\), \(EB=\qty{9}{\centi\m}\) ja $AB= (joonis 4.22. \[\frac{6}{15}=\frac{DE}{\blank{AB}}.\] Lõigu \(DE\) pikkus on .
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Mõõtmisel saadi, et korrapärase kuusnurga \(ABCDEF\) ühe külje pikkus on ligikaudu ja apoteem on ligikaudu (joonis 4.21).Lõigu \(AB\) ligikaudne pikkus on Lõigu \(OH\) ligikaudne pikkus on Kuusnurga \(ABCDEF\) ligikaudne ümbermõõt on Kolmnurga \(ABO\) ligikaudne pindala on . Kuusnurga \(ABCDEF\) ligikaudne pindala on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.11 on olemas trapetsi kõikide külgede pikkused ja kõikid ekülgede keskpunktid.Joonesta trapetsi kesklõik!
Arvuta kesklõigu \(K\) pikkus! Märgista, kui väide on õige!
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.2 Test: 2. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on diskreetsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on mood?
2. taseme ülesanne: Esita näide ulatuse kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite maksimum?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on tulpdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on karjamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Täida tabel 4.3.
Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, korrutan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \(2(a-b)-(3a+b)=\)Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[(x-3y)^2=x^2\blank{-6}xy+9y^2.\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: Täida lünk nii, et võrrandi lahend oleks \(x=1\):
\(2x+4=\blank{7}-x\).
Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Lineaarfunktsioonide \(y=ax-3\) ja \(y=4x+3\) graafikud on paralleelsed, kui lineaarliikme kordaja \(a=\)Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Kaks kolmnurka on sarnased, kuiÕpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.10 kujutatud kujund koosneb trapetsist \(ABDE\) ja kolmnurgast \(BCD\). Joonesta trapetsile punktist \(A\) kõrgus!Arvuta kujundi pindala!
Trapetsi pikem alus on
Trapetsi pindala on
Kujundi \(ABCD\) pindala on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.12 on trapetsikujuline maatükk, mille pikem alus on . Mööda trapetsikujulise maatüki kesklõiku jookseb kuivenduskraav. Naabrite majad paiknevad trapetsi tippudes nii, et kõige lühem jalgtee naabrini läheb mööda trapetsi diagonaali. Kuivenduskraav ja jalgtee lõikuvad nii, et lühem osa kuivenduskraavist on (vaata joonist). Veel on teada, et maatüki kahe paralleelse külje vaheline kaugus on .Märgista, kui väide on õige:
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.3 Test: 3. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on jätkuvad andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on mediaan?
2. taseme ülesanne: Esita näide miinimumi kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite ulatus?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on punktdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on metsamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: \((5^{\blank{2}})^4 = 5^8.\)
Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \[\begin{cases} x = -1 \\ y = -2 \end{cases} \rightarrow 2x^2 y+3xy+5y=\]Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[(7+m)(m-7)=m^2\blank{-49}.\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: \(\begin{cases} 4x+6y=10\\ 2x+3y=4|\cdot (-2) \end{cases} \rightarrow +\begin{cases} 4x+6y=10\\ -4x-6y=-8 \end{cases} \rightarrow 0x+0y=2.\) Märgista õige väide:Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.26 on kahe tundmatuga lineaarvõrrandisüsteeme kujutatud graafiliselt. Märgista iga õige väide sinu poolt vaadates vasema lineaarvõrrandisüsteemi kohta: Märgista iga õige väide sinu poolt vaadates parempoolse lineaarvõrrandisüsteemi kohta:Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Joonisel 4.23 on kolmurgad \(ABC\) ja \(DFE\) sarnased. Millised tunnuse järgi on kolmurgad sarnased?Arvuta sarnasustegur \(k\) ja lõigu \(EF\) pikkus! \[k=\blank{\frac{2}{3}}; EF=\blank{6}\ensuremath{\thinspace}\unit{\centi\m}.\]
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Vaata joonist 4.14 ja vali õige valikvastus!Joonisel on
\(ABCDE\). Joonesta viisnurgale diagonaalid punktist \(A\). Viisnurga sisenurkade summa arvutatakse avaldise \((\blank{n-2}) \cdot 180 \degree\) abil.
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Kolmnurga külgede pikkused on , ja . Arvuta kolmnurga kesklõikudest moodustatud kolmnurga ümbermõõt!Kesklõikudest moodustunud komnurga ümbermõõt on \(P=\)
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.4 Test: 4. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on kvalitatiivsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on miinimum?
2. taseme ülesanne: Esita näide moe kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite miinimum?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on joondiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on põllumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne \(\frac{1}{2}\):Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida veerand arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Vali alljärgnevatest avaldistest üksliikme \(4x^2 \cdot (-xy) \cdot (-y)\) normaalkuju:Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[18x^2y+2y=\blank{2}y(9x^2+\blank{1}).\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: On antud võrrand \(5x+7=x-1\). Milline arv on selle võrrandi lahendiks?Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.13 on kahe funktsiooni graafikud. Sinine graafik esindab funktsiooni Oranž graafik esindab funktsiooniÕpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Sarnaste hulknurkadega ümbermõõtude suhe võrdub Kahe sarnase hulknurga ümbermõõdud on ja . Kuidas suhtuvad nende hulknurkade pindalad?Hulknurkade pindalade suhe võrdub
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.16 on romb \(ABCD\).Uuri joonist ja märgista, kui väide on tõene:
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.8 on kolmnurk \(ABC\), millesse on joonestatud lõik \(a\). Uuri joonist ning vali õiged väited valikvastuste seast lõigu \(a\) kohta ja täida lünk:Lõik \(a\) on kolmnurga \(ABC\)
Lõik \(a\) on kolmnurga
Lõigu \(a\) pikkus on
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.5 Test: 5. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Millised on andmete liigid?
Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on ulatus?
2. taseme ülesanne: Esita näide aritmeetilise keskmise kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite mediaan?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on sektordiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on elamumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, korrutan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Avaldist \(2x+3y-3x-5y\) nimetatakse\(2x+3y-3x-5y=\blank{-}x-2{y}.\)
Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \((m-n)^2=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: On antud kahe tundmatuga lineaarvõrrand \(3x-4y=2\). Milline arvupaar sobib võrrandi lahendiks?Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Lineaarfunktsioonide \(y=ax-3\) ja \(y=4x+3\) graafikud on paralleelsed, kui lineaarliikme kordaja \(a=\)Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Joonisel 4.24 on nelinurkse maatüki plaan plaanimõõduga 1 : 500. Selle maatüki \(ABCD\) ümbermõõt plaanil on ja pindala . Arvuta maatüki tegelik ümbermõõt meetrites \(P\) ja pindala ruutmeetrites \(S\):Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Rombi diagonaalide pikkused on ja .Rombi pindala on
.
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.11 on olemas trapetsi kõikide külgede pikkused ja kõikid ekülgede keskpunktid.Joonesta trapetsi kesklõik!
Arvuta kesklõigu \(K\) pikkus! Märgista, kui väide on õige!
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.6 Test: 6. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on kvantitatiivsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on aritmeetiline keskmine?
2. taseme ülesanne: Esita näide maksimumi kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite aritmeetiline keskmine?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on tulpdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on karjamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Täida tabel 4.3.
Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: \((5^{\blank{2}})^4 = 5^8.\)
Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \(2(a-b)-(3a+b)=\)Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \((n-m)(m+n)=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: Lahenda võrrand \(7-3y=10\)! Võrrandi lahend onÕpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.26 on kahe tundmatuga lineaarvõrrandisüsteeme kujutatud graafiliselt. Märgista iga õige väide sinu poolt vaadates vasema lineaarvõrrandisüsteemi kohta: Märgista iga õige väide sinu poolt vaadates parempoolse lineaarvõrrandisüsteemi kohta:Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Võrdhaarses kolmnurgas \(ABC\) on \(DE \parallel AB\), \(CD=\qty{6}{\centi\m}\), \(EB=\qty{9}{\centi\m}\) ja $AB= (joonis 4.22. \[\frac{6}{15}=\frac{DE}{\blank{AB}}.\] Lõigu \(DE\) pikkus on .
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.15 on rööpkülik \(KLMN\).Rööpküliku külje \(KN\) pikkus on , ja nurga \(N\) suurus on Joonesta rööpkülikule punktist \(N\) kõrgus!
Kui kujundi kõrgus on \(h=\qty{2,4}{\centi\m}\), siis kujundi pindala \(S=\)
.
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.12 on trapetsikujuline maatükk, mille pikem alus on . Mööda trapetsikujulise maatüki kesklõiku jookseb kuivenduskraav. Naabrite majad paiknevad trapetsi tippudes nii, et kõige lühem jalgtee naabrini läheb mööda trapetsi diagonaali. Kuivenduskraav ja jalgtee lõikuvad nii, et lühem osa kuivenduskraavist on (vaata joonist). Veel on teada, et maatüki kahe paralleelse külje vaheline kaugus on .Märgista, kui väide on õige:
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.7 Test: 7. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Nimeta üks andmete kogumise meetod!
Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on maksimum?
2. taseme ülesanne: Esita näide mediaani kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite mood?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on punktdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on metsamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida veerand arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \[\begin{cases} x = -1 \\ y = -2 \end{cases} \rightarrow 2x^2 y+3xy+5y=\]Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \((m+n)(m+n)=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: \[-2x-y=-7.\] \[y=\]\[x=-3 \rightarrow y=\blank{13}.\]
Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.13 on kahe funktsiooni graafikud. Sinine graafik esindab funktsiooni Oranž graafik esindab funktsiooniÕpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Kaks kolmnurka on sarnased, kuiÕpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.9 on kolmnurk \(KLM\). Selle kolmnurga raskuskeset märgib joonisel punkt \(O\). Joonesta kolmnurgale mediaanid tippudest \(M\) ja \(L\)!Kolmnurga mediaanide lõikepunkt jaotab mediaanid kaheks osaks: küljepoolseks ja tipupoolseks osaks. Küljele \(KM\) tõmmatud mediaanist tipupoolne osa on pikkune. Arvuta mediaani kogupikkus!
Küljele \(KM\) tõmmatud mediaani pikkus on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Kolmnurga külgede pikkused on , ja . Arvuta kolmnurga kesklõikudest moodustatud kolmnurga ümbermõõt!Kesklõikudest moodustunud komnurga ümbermõõt on \(P=\)
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.8 Test: 8. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on diskreetsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on mood?
2. taseme ülesanne: Esita näide ulatuse kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite maksimum?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on joondiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on põllumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne \(\frac{1}{2}\):Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, korrutan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Vali alljärgnevatest avaldistest üksliikme \(4x^2 \cdot (-xy) \cdot (-y)\) normaalkuju:Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: Joonisel 4.25 esitatud kujundi pindala lihtsustatud avaldis on \[S=\blank{(m+3)^2}\] \[\blank{-(m+2)(m-3)}\] \[\blank{=7m+15}.\] Arvuta kujundi pindala, kui \(m=\frac{2}{7}\, \unit{\centi\m}\). Kujundi pindala on \(S=\blank{17}\unit{\square\centi\m}\).
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: On antud kahe tundmatuga lineaarvõrrandidüsteem: \(\begin{cases} 2x+y=5\\ 3x-2y=4 \end{cases}\). Milline arvupaar sobib süsteemi lahendiks?Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Lineaarfunktsioonide \(y=ax-3\) ja \(y=4x+3\) graafikud on paralleelsed, kui lineaarliikme kordaja \(a=\)Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Joonisel 4.23 on kolmurgad \(ABC\) ja \(DFE\) sarnased. Millised tunnuse järgi on kolmurgad sarnased?Arvuta sarnasustegur \(k\) ja lõigu \(EF\) pikkus! \[k=\blank{\frac{2}{3}}; EF=\blank{6}\ensuremath{\thinspace}\unit{\centi\m}.\]
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Mõõtmisel saadi, et korrapärase kuusnurga \(ABCDEF\) ühe külje pikkus on ligikaudu ja apoteem on ligikaudu (joonis 4.21).Lõigu \(AB\) ligikaudne pikkus on Lõigu \(OH\) ligikaudne pikkus on Kuusnurga \(ABCDEF\) ligikaudne ümbermõõt on Kolmnurga \(ABO\) ligikaudne pindala on . Kuusnurga \(ABCDEF\) ligikaudne pindala on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.8 on kolmnurk \(ABC\), millesse on joonestatud lõik \(a\). Uuri joonist ning vali õiged väited valikvastuste seast lõigu \(a\) kohta ja täida lünk:Lõik \(a\) on kolmnurga \(ABC\)
Lõik \(a\) on kolmnurga
Lõigu \(a\) pikkus on
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.9 Test: 9. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on jätkuvad andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on mediaan?
2. taseme ülesanne: Esita näide miinimumi kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite ulatus?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on sektordiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on elamumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: \((5^{\blank{2}})^4 = 5^8.\)
Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Avaldist \(2x+3y-3x-5y\) nimetatakse\(2x+3y-3x-5y=\blank{-}x-2{y}.\)
Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \(m^2-n^2=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: \(x=1 \rightarrow 2x+4=\)\[-x.\]
Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.26 on kahe tundmatuga lineaarvõrrandisüsteeme kujutatud graafiliselt. Märgista iga õige väide sinu poolt vaadates vasema lineaarvõrrandisüsteemi kohta: Märgista iga õige väide sinu poolt vaadates parempoolse lineaarvõrrandisüsteemi kohta:Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Sarnaste hulknurkadega ümbermõõtude suhe võrdub Kahe sarnase hulknurga ümbermõõdud on ja . Kuidas suhtuvad nende hulknurkade pindalad?Hulknurkade pindalade suhe võrdub
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.10 kujutatud kujund koosneb trapetsist \(ABDE\) ja kolmnurgast \(BCD\). Joonesta trapetsile punktist \(A\) kõrgus!Arvuta kujundi pindala!
Trapetsi pikem alus on
Trapetsi pindala on
Kujundi \(ABCD\) pindala on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.11 on olemas trapetsi kõikide külgede pikkused ja kõikid ekülgede keskpunktid.Joonesta trapetsi kesklõik!
Arvuta kesklõigu \(K\) pikkus! Märgista, kui väide on õige!
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.10 Test: 10. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on kvalitatiivsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on miinimum?
2. taseme ülesanne: Esita näide moe kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite miinimum?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on tulpdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on karjamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Täida tabel 4.3.
Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida veerand arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \(2(a-b)-(3a+b)=\)Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[3x^2(\] \[xy-4y+5)=-36x^3y-\]\[x^2y+15x^2.\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: Lahenda võrrand \(0,5x+4=5\)! Võrrandi lahend onÕpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.13 on kahe funktsiooni graafikud. Sinine graafik esindab funktsiooni Oranž graafik esindab funktsiooniÕpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Joonisel 4.24 on nelinurkse maatüki plaan plaanimõõduga 1 : 500. Selle maatüki \(ABCD\) ümbermõõt plaanil on ja pindala . Arvuta maatüki tegelik ümbermõõt meetrites \(P\) ja pindala ruutmeetrites \(S\):Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Vaata joonist 4.14 ja vali õige valikvastus!Joonisel on
\(ABCDE\). Joonesta viisnurgale diagonaalid punktist \(A\). Viisnurga sisenurkade summa arvutatakse avaldise \((\blank{n-2}) \cdot 180 \degree\) abil.
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.12 on trapetsikujuline maatükk, mille pikem alus on . Mööda trapetsikujulise maatüki kesklõiku jookseb kuivenduskraav. Naabrite majad paiknevad trapetsi tippudes nii, et kõige lühem jalgtee naabrini läheb mööda trapetsi diagonaali. Kuivenduskraav ja jalgtee lõikuvad nii, et lühem osa kuivenduskraavist on (vaata joonist). Veel on teada, et maatüki kahe paralleelse külje vaheline kaugus on .Märgista, kui väide on õige:
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.11 Test: 11. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Millised on andmete liigid?
Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on ulatus?
2. taseme ülesanne: Esita näide aritmeetilise keskmise kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite mediaan?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on punktdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on metsamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, korrutan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \[\begin{cases} x = -1 \\ y = -2 \end{cases} \rightarrow 2x^2 y+3xy+5y=\]Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[(x-3y)^2=x^2\blank{-6}xy+9y^2.\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: Võrrandi \(\frac{5x-2}{5}=x+1\) lahendamisel korrutatakse võrrandi mõlemat poolt arvuga 5: \[\frac{5x-2}{5}=x+1|\cdot 5.\] Millise võrrandi saad? Kirjuta lünkadesse sobivad arvud: \[\blank{5}x-\blank{2}=\blank{5}x+5\]. Milline allpool olevatest lausetest esitab saadud võrrandi lahendit?Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Lineaarfunktsioonide \(y=ax-3\) ja \(y=4x+3\) graafikud on paralleelsed, kui lineaarliikme kordaja \(a=\)Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Võrdhaarses kolmnurgas \(ABC\) on \(DE \parallel AB\), \(CD=\qty{6}{\centi\m}\), \(EB=\qty{9}{\centi\m}\) ja $AB= (joonis 4.22. \[\frac{6}{15}=\frac{DE}{\blank{AB}}.\] Lõigu \(DE\) pikkus on .
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.16 on romb \(ABCD\).Uuri joonist ja märgista, kui väide on tõene:
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Kolmnurga külgede pikkused on , ja . Arvuta kolmnurga kesklõikudest moodustatud kolmnurga ümbermõõt!Kesklõikudest moodustunud komnurga ümbermõõt on \(P=\)
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.12 Test: 12. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on kvantitatiivsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on aritmeetiline keskmine?
2. taseme ülesanne: Esita näide maksimumi kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite aritmeetiline keskmine?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on joondiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on põllumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne \(\frac{1}{2}\):Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: \((5^{\blank{2}})^4 = 5^8.\)
Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Vali alljärgnevatest avaldistest üksliikme \(4x^2 \cdot (-xy) \cdot (-y)\) normaalkuju:Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[(7+m)(m-7)=m^2\blank{-49}.\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: \(\begin{cases} 3x-4y=15\\ 2x-4y=-10 \end{cases} \rightarrow\)Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.26 on kahe tundmatuga lineaarvõrrandisüsteeme kujutatud graafiliselt. Märgista iga õige väide sinu poolt vaadates vasema lineaarvõrrandisüsteemi kohta: Märgista iga õige väide sinu poolt vaadates parempoolse lineaarvõrrandisüsteemi kohta:Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Kaks kolmnurka on sarnased, kuiÕpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Rombi diagonaalide pikkused on ja .Rombi pindala on
.
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.8 on kolmnurk \(ABC\), millesse on joonestatud lõik \(a\). Uuri joonist ning vali õiged väited valikvastuste seast lõigu \(a\) kohta ja täida lünk:Lõik \(a\) on kolmnurga \(ABC\)
Lõik \(a\) on kolmnurga
Lõigu \(a\) pikkus on
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.13 Test: 13. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Nimeta üks andmete kogumise meetod!
Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on maksimum?
2. taseme ülesanne: Esita näide mediaani kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite mood?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on sektordiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on elamumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida veerand arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Avaldist \(2x+3y-3x-5y\) nimetatakse\(2x+3y-3x-5y=\blank{-}x-2{y}.\)
Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \[18x^2y+2y=\blank{2}y(9x^2+\blank{1}).\]
Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: Täida lünk nii, et võrrandi lahend oleks \(x=1\):
\(2x+4=\blank{7}-x\).
Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.13 on kahe funktsiooni graafikud. Sinine graafik esindab funktsiooni Oranž graafik esindab funktsiooniÕpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Joonisel 4.23 on kolmurgad \(ABC\) ja \(DFE\) sarnased. Millised tunnuse järgi on kolmurgad sarnased?Arvuta sarnasustegur \(k\) ja lõigu \(EF\) pikkus! \[k=\blank{\frac{2}{3}}; EF=\blank{6}\ensuremath{\thinspace}\unit{\centi\m}.\]
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.15 on rööpkülik \(KLMN\).Rööpküliku külje \(KN\) pikkus on , ja nurga \(N\) suurus on Joonesta rööpkülikule punktist \(N\) kõrgus!
Kui kujundi kõrgus on \(h=\qty{2,4}{\centi\m}\), siis kujundi pindala \(S=\)
.
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.11 on olemas trapetsi kõikide külgede pikkused ja kõikid ekülgede keskpunktid.Joonesta trapetsi kesklõik!
Arvuta kesklõigu \(K\) pikkus! Märgista, kui väide on õige!
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.14 Test: 14. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on diskreetsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on mood?
2. taseme ülesanne: Esita näide ulatuse kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite maksimum?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on tulpdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on karjamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Täida tabel 4.3.
Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, korrutan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \(2(a-b)-(3a+b)=\)Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \((m-n)^2=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: \(\begin{cases} 4x+6y=10\\ 2x+3y=4|\cdot (-2) \end{cases} \rightarrow +\begin{cases} 4x+6y=10\\ -4x-6y=-8 \end{cases} \rightarrow 0x+0y=2.\) Märgista õige väide:Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Lineaarfunktsioonide \(y=ax-3\) ja \(y=4x+3\) graafikud on paralleelsed, kui lineaarliikme kordaja \(a=\)Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Sarnaste hulknurkadega ümbermõõtude suhe võrdub Kahe sarnase hulknurga ümbermõõdud on ja . Kuidas suhtuvad nende hulknurkade pindalad?Hulknurkade pindalade suhe võrdub
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.9 on kolmnurk \(KLM\). Selle kolmnurga raskuskeset märgib joonisel punkt \(O\). Joonesta kolmnurgale mediaanid tippudest \(M\) ja \(L\)!Kolmnurga mediaanide lõikepunkt jaotab mediaanid kaheks osaks: küljepoolseks ja tipupoolseks osaks. Küljele \(KM\) tõmmatud mediaanist tipupoolne osa on pikkune. Arvuta mediaani kogupikkus!
Küljele \(KM\) tõmmatud mediaani pikkus on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.12 on trapetsikujuline maatükk, mille pikem alus on . Mööda trapetsikujulise maatüki kesklõiku jookseb kuivenduskraav. Naabrite majad paiknevad trapetsi tippudes nii, et kõige lühem jalgtee naabrini läheb mööda trapetsi diagonaali. Kuivenduskraav ja jalgtee lõikuvad nii, et lühem osa kuivenduskraavist on (vaata joonist). Veel on teada, et maatüki kahe paralleelse külje vaheline kaugus on .Märgista, kui väide on õige:
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.15 Test: 15. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on jätkuvad andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on mediaan?
2. taseme ülesanne: Esita näide miinimumi kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite ulatus?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli ühtlasema tasemega?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on punktdiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on metsamaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne :Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Sügisel maksis kartuleid senti ja kevadel senti. Mitme protsendi võrra tõusis kartuli hind?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: \((5^{\blank{2}})^4 = 5^8.\)
Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \[1\frac{2}{3}\cdot(-0,3)=\]Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: \[\begin{cases} x = -1 \\ y = -2 \end{cases} \rightarrow 2x^2 y+3xy+5y=\]Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(\frac{1}{3}-0,5=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \((n-m)(m+n)=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: Kui kaks sirget \(s\) ja \(t\) on paralleelsed, siisVastav joonis on
Õpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.18 on ringjoon, mille keskpunkt asetseb punktis \(C\).
Arvuta nurkade \(KNL\) ja \(KML\) suurus, kui \(\angle KCL=\ang{28}\).
\(\angle KNL=\blank{\ang{14}}, \angle KML=\blank{\ang{14}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vai võrrandiga \(\frac{2}{x} = \frac{7}{3}\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: On antud võrrand \(5x+7=x-1\). Milline arv on selle võrrandi lahendiks?Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Raamat ja kaustik maksavad kokku . Raamatulaadal oli sama raamatu hinda alandatud võrra ja sama kaustiku hinda poole võrra. Nüüd maksid raamat ja kaustik kokku . Koosta nende tingimuste järgi kahe tundmatuga normaalkujuline lineaarvõrrandisüsteem, kus raamatu hind on \(x\), ja vihiku hind \(y\), . Märgista sobilik lahendus:Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Uuri tabelit 4.1 ja otsusta, milline võrdus esitab seost muutujate \(x\) ja \(y\) vahel:Millises punktis lõikab funktsiooni \(y=-2x-5\) graafik \(y\)-telge?
Funktsiooni graafik lõikab \(y\)-telge punktis (; ).
Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.26 on kahe tundmatuga lineaarvõrrandisüsteeme kujutatud graafiliselt. Märgista iga õige väide sinu poolt vaadates vasema lineaarvõrrandisüsteemi kohta: Märgista iga õige väide sinu poolt vaadates parempoolse lineaarvõrrandisüsteemi kohta:Õpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Joonisel 4.24 on nelinurkse maatüki plaan plaanimõõduga 1 : 500. Selle maatüki \(ABCD\) ümbermõõt plaanil on ja pindala . Arvuta maatüki tegelik ümbermõõt meetrites \(P\) ja pindala ruutmeetrites \(S\):Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Mõõtmisel saadi, et korrapärase kuusnurga \(ABCDEF\) ühe külje pikkus on ligikaudu ja apoteem on ligikaudu (joonis 4.21).Lõigu \(AB\) ligikaudne pikkus on Lõigu \(OH\) ligikaudne pikkus on Kuusnurga \(ABCDEF\) ligikaudne ümbermõõt on Kolmnurga \(ABO\) ligikaudne pindala on . Kuusnurga \(ABCDEF\) ligikaudne pindala on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Kolmnurga külgede pikkused on , ja . Arvuta kolmnurga kesklõikudest moodustatud kolmnurga ümbermõõt!Kesklõikudest moodustunud komnurga ümbermõõt on \(P=\)
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(\num{0.0001}=10^{\blank{-4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.1.16 Test: 16. õpilane
Õpilane teab andmete liike ja andmete kogumise erinevaid meetodeid (mõõtmine, küsimustik).
1. taseme ülesanne: Vaata allolevaid väiteid ja märgi, millised nendest on kvalitatiivsed andmed:Õpilane iseloomustab andmestikku aritmeetilise keskmise, mediaani, moodi, miinimumi, maksimumi ja ulatuse järgi.
1. taseme ülesanne: Mis on miinimum?
2. taseme ülesanne: Esita näide moe kohta!
3. taseme ülesanne: Õpetaja telefoniaadress on 56204556. Milline on nende numbrite miinimum?
4. taseme ülesanne: Kahe rühma kontrolltöö punktisummad olid:
- rühm A: 6, 7, 7, 8, 9,
- rühm B: 3, 5, 7, 9, 11.
Võrdle tulemusi ja analüüsi: kumb rühm oli keskmiselt tugevam?
Õpilane loeb, mõistab ja selgitab andmeid tabelist, tulp-, sektor-, joon- ja punktdiagrammilt.
1. taseme ülesanne: Mis on joondiagramm?
3. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Vaata sektordiagrammi joonist 4.1 ja märgi, kui palju on põllumaad:4. taseme ülesanne: Roosioksa talu pererahval on põllumaad , karjamaad , metsamaad ja elamumaad . Kirjuta sektordiagrammile joonisel 4.1 erinevate maatükkide suurused protsentides!
Õpilane teisendab protsendi kümnendmurruks ja harilikuks murruks ning vastupidi.
3. taseme ülesanne: Märgi kõik arvud, millega on võrdne \(\frac{1}{2}\):Õpilane kasutab protsentarvutusel erinevaid lahendusmeetodeid (ühikumeetod, võrre, skeem, algoritm).
3. taseme ülesanne: Et leida veerand arvust, jagan arvu:Õpilane lahendab protsentarvutuse tüüpülesandeid (osa leidmine, terviku leidmine, osamäära leidmine, suuruse muutumine).
3. taseme ülesanne: Mari ostis eurot maksva jäätise, ta kasutas selleks oma taskuvaluutat. Kui palju oli Maril taskuvaluutat?Õpilane kasutab protsentarvutust otsuse tegemiseks ja põhjendamiseks (nt laen, hoius, intress, maksud, investeerimine).
5. taseme ülesanne: Raamatu Eesti reisijuht hind enne allahindlust oli \(\qty{20}{\euro}\). Kauba hinna muutus on esitatud pildil 4.2. Marial oli eurot. Kas Maria saab selle raamatu osta?Õpilane selgitab naturaalarvulise astendajaga astendamise tähendust (E).
2. taseme ülesanne: Mida tähendab \(4^2\)?
Õpilane põhjendab ja kasutab astendamisreegleid.
4. taseme ülesanne: Milline väide on tõene?Õpilane liidab, lahutab, korrutab, jagab ja astendab naturaalarvulise astendajaga ratsionaalarve peast, kirjalikult ja taskuarvutiga ning rakendab tehete järjekorda.
4. taseme ülesanne: \(-(-4)^0=\)Õpilane korrastab üks- ja hulkliikmeid, liidab, lahutab ning korrutab üks- ja hulkliikmeid ning jagab üksliikmeid ja hulkliiget üksliikmega.
3. taseme ülesanne: Vali alljärgnevatest avaldistest üksliikme \(4x^2 \cdot (-xy) \cdot (-y)\) normaalkuju:Õpilane lihtsustab kahetehtelisi ratsionaalavaldisi.
3. taseme ülesanne: \(-6 + 13+6-20-7=\)Õpilane tegurdab hulkliikmeid (toob teguri sulgude ette, kasutab ja põhjendab ruutude vahe, summa ruudu ja vahe ruudu abivalemeid, tegurdab ruutkolmliiget).
4. taseme ülesanne: \((m+n)(m+n)=\)Õpilane teab põik- ja lähisnurkade mõisteid ja nende nurkade seoseid paralleelsete sirgete korral.
1. taseme ülesanne: Joonisel 4.3 on näidatud kahe sirge lõikamisel kolmanda sirgega tekkinud nurgad.Nurgad ja \(\alpha\) on
Nurk \(\alpha=\)
Nurgad ja \(\beta\) on
Nurk \(\beta=\)
Õpilane põhjendab ja kasutab sirgete paralleelsuse tunnuseid.
4. taseme ülesanne: siis on kaks sirget \(s\) ja \(t\) paralleelsed ja vastav joonis onÕpilane joonestab ja konstrueerib (käsitsi ja arvutiga) tasandilisi kujundeid (korrapärane hulknurk, kolmnurk, rööpkülik, trapets, ring) etteantud elementide järgi korrapärase hulknurga ja kolmnurga sise-ja ümberringjoone.
3. taseme ülesanne: Märgi joonisele 4.20, kus on kolmnurga küljepoolitajad, nurgapoolitajad, külgede keskristsirged, punkt \(C\) siseringjoone keskpunktina, ümberringjoone keskpunktina, mediaanide lõikepunktina!
Õpilane teab kesk- ja piirdenurga mõisteid ning nendevahelist seost.
1. taseme ülesanne: Joonisel 4.17 on ringjoon keskpunktiga \(O\).\(\angle CAB\) on
nurk.
Kui \(\angle CAB=\ang{30}\), siis \(\angle COB=\blank{\ang{60}}\).
Õpilane teab ringjoone puutuja mõistet ja omadust.
1. taseme ülesanne: Joonisel 4.19 on ringjoonele keskpunktiga \(C\) joonestatud kaks puutujat \(LK\) ja \(LM\). Märgista iga õige väide!Õpilane nimetab võrrandi põhiomadusi.
1. taseme ülesanne: Vali võrrandiga \(x-5=9\) samaväärne võrrand:Õpilane selgitab eluliste näidete põhjal võrdelise, lineaarse ja pöördvõrdelise sõltuvuse tähendust.
2. taseme ülesanne: Kauba ühe kilogrammi hind on .Kauba koguhinna \(y\) ja kauba koguse \(x\) vahel esitub seos \(y=\)
Õpilane lahendab lineaar- ja võrdekujulisi võrrandeid ning lineaarvõrrandisüsteeme kasutades võrrandi põhiomadusi (sh graafiliselt ning arvutiprogrammide abil).
3. taseme ülesanne: On antud kahe tundmatuga lineaarvõrrand \(3x-4y=2\). Milline arvupaar sobib võrrandi lahendiks?Õpilane koostab ja lahendab tekstülesandeid, mis lahenduvad võrrandi või võrrandisüsteemi abil (sh võrdelise jaotamise ülesandeid).
6. taseme ülesanne: Loe teksti ja koosta tekstile vastav võrrand:
Kolm sõpra Markus, Tõnis ja Karl kulutasid poes taskuvaluutat. Markusel jäi pärast poes käiku valuutat alles euro võrra vähem kui Karlil. Karlil jäi valuutat alles kaks korda rohkem kui Tõnisel. Kokku jäi poistel valuutat alles eurot.
Koosta võrrand, mis näitab, kui palju valuutat jäi kokku sõpradel alles peale poes käiku, kui Karlil alles jäänud valuuta hulka esitab arv \(x\):
\[\underbrace{\blank{x-4,5}}_\text{Markus}+\underbrace{x}_\text{Karl}+\underbrace{\blank{\frac{x}{4}}}_\text{Tõnis}=49,5.\]
Lahenda saadud võrrand ning kirjuta välja võrrandi lahend!
Võrrandi lahend on \(x=\blank{24}\).
Õpilane joonestab etteantud funktsiooni graafiku (sirge, hüperbooli, parabooli) (nii käsitsi kui ka arvutiprogrammiga) ning loeb graafikult funktsiooni ja argumendi väärtusi.
3. taseme ülesanne: Millist seost esitab valem \(y=-2x-5\)?Õpilane selgitab arvutiga tehtud dünaamilisi jooniseid kasutades funktsiooni graafiku asendi ja kuju sõltuvust funktsiooni avaldises olevatest kordajatest (ruutfunktsiooni korral ainult ruutliikme kordajast ja vabaliikmest).
4. taseme ülesanne: Joonisel 4.13 on kahe funktsiooni graafikud. Sinine graafik esindab funktsiooni Oranž graafik esindab funktsiooniÕpilane kasutab probleemülesannete lahendamiseks hulknurkade sarnasust (nt maa-alade plaanistamine).
4. taseme ülesanne: Võrdhaarses kolmnurgas \(ABC\) on \(DE \parallel AB\), \(CD=\qty{6}{\centi\m}\), \(EB=\qty{9}{\centi\m}\) ja $AB= (joonis 4.22. \[\frac{6}{15}=\frac{DE}{\blank{AB}}.\] Lõigu \(DE\) pikkus on .
Õpilane arvutab tasandiliste kujundite (korrapärane hulknurk, kolmnurk, rööpkülik, romb, trapets, ring) joonelemendid, ümbermõõdu, pindala.
3. taseme ülesanne: Joonisel 4.10 kujutatud kujund koosneb trapetsist \(ABDE\) ja kolmnurgast \(BCD\). Joonesta trapetsile punktist \(A\) kõrgus!Arvuta kujundi pindala!
Trapetsi pikem alus on
Trapetsi pindala on
Kujundi \(ABCD\) pindala on
Õpilane arvutab ruumiliste kujundite (püstprisma, püramiid, silinder, koonus, kera) joonelemendid, pindala ja ruumala.
3. taseme ülesanne: Pealt lahtise risttahukakujulise anuma ruudukujulise põhja ühe serva pikkus on . Anuma kõrgus on . Mitu liitrit vett mahutab see anum?.
Õpilane teab kolmnurga ja trapetsi kesklõigu mõistet ning nende omadusi.
1. taseme ülesanne: Joonisel 4.8 on kolmnurk \(ABC\), millesse on joonestatud lõik \(a\). Uuri joonist ning vali õiged väited valikvastuste seast lõigu \(a\) kohta ja täida lünk:Lõik \(a\) on kolmnurga \(ABC\)
Lõik \(a\) on kolmnurga
Lõigu \(a\) pikkus on
Õpilane kirjutab suuri ja väikseid arve standardkujul.
4. taseme ülesanne: \(100000=10^{\blank{4}}.\)
Õpilane eristab hüpoteesi, eeldust, väidet ja tõestust, selgitab mõne teoreemi tõestuskäiku, vajaduse korral tuletab lihtsamaid valemeid.
4. taseme ülesanne: Rööpkülikuks nimetatakse nelinurka, mille Teoreemi sõnastuses teoreemi eeldus algab sõnaga ja teoreemi väide algab sõnaga4.3 Tabelid
| 1 | 2 | 3 | |
|---|---|---|---|
| x | -4 | 2 | 3 |
| y | 3 | -6 | -4 |
| Harilik osamäär | Kümnendosamäär | Protsentides |
|---|---|---|
| \(\frac{1}{2}\) | \(\num{0,5}\) | |
| \(\frac{1}{4}\) | \(\blank{\num{0,25}}\) | |
| \(\blank{\frac{2}{5}}\) | \(\num{0,4}\) | |
| \(\blank{\frac{3}{4}}\) | \(\num{0,75}\) |
4.4 Joonised
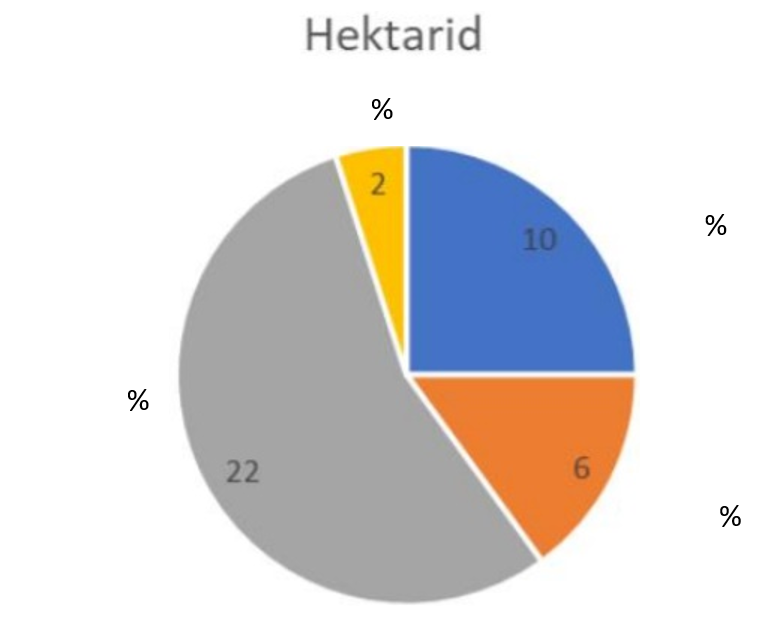
Figure 4.1: Roosioksa talu pererahva maade jaotus.

Figure 4.2: Allahinnatud raamat.
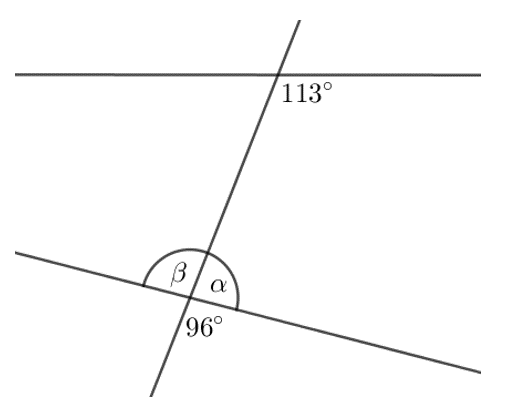
Figure 4.3: Kahe sirge lõikamisel kolmandaga nurgad.
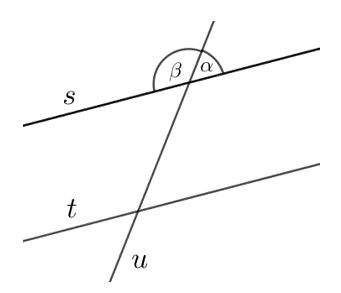
Figure 4.4: Kahe sirge lõikamisel kolmandaga kõrvunurgad.
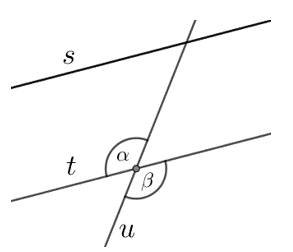
Figure 4.5: Kahe sirge lõikamisel kolmandaga tippnurgad.
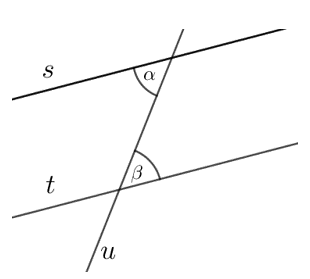
Figure 4.6: Kahe sirge lõikamisel kolmandaga põiknurgad.
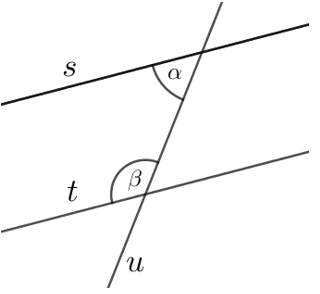
Figure 4.7: Kahe sirge lõikamisel kolmandaga lähisnurgad.
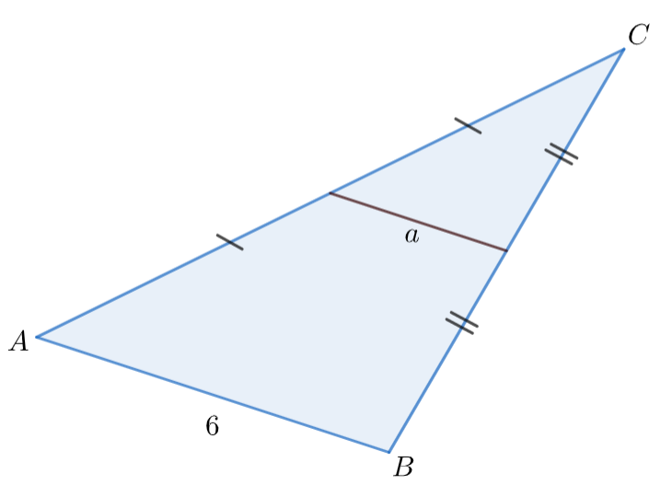
Figure 4.8: Kolmnurga teatud lisajoon.
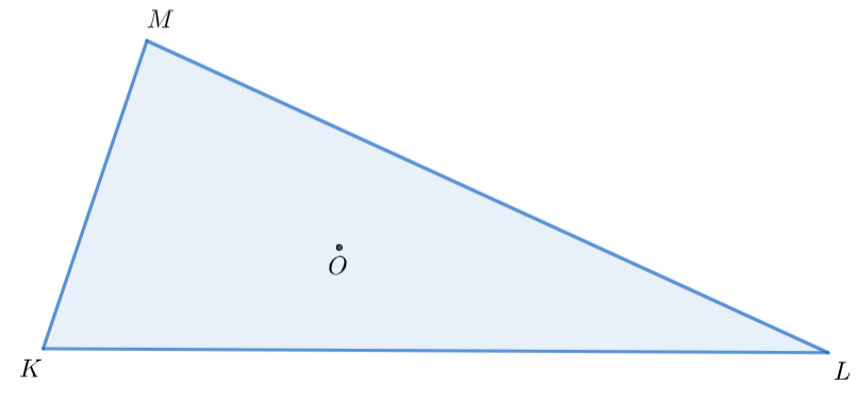
Figure 4.9: Kolmnurga raskuskese.
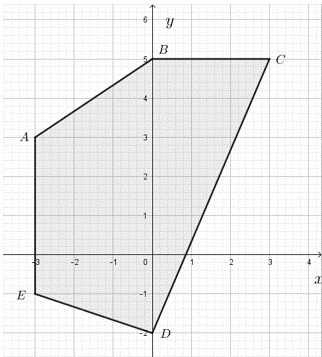
Figure 4.10: Kolmnurgast ja trapetsist moodustuv kujund.
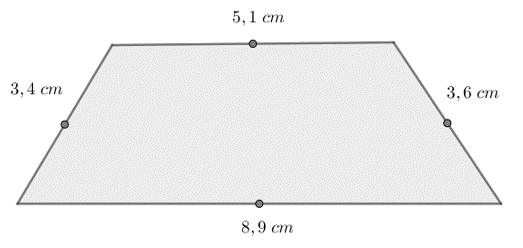
Figure 4.11: Trapets kesklõiguta.
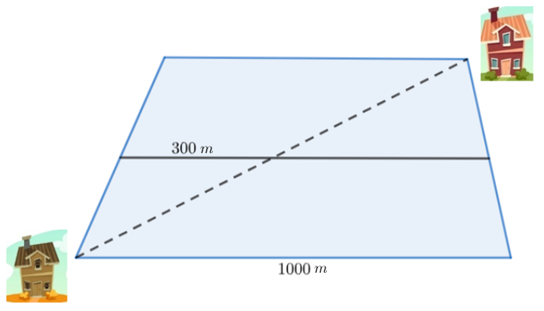
Figure 4.12: Trapets diagonaaliga.
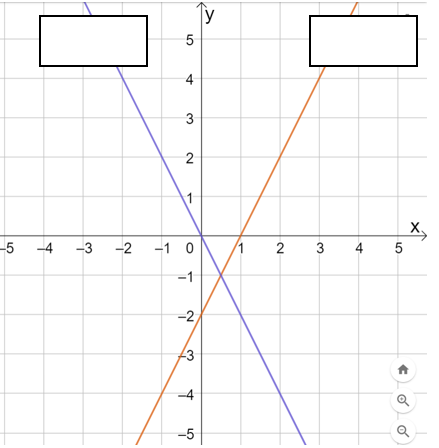
Figure 4.13: Lineaarsed graafikud.
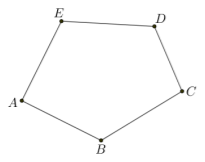
Figure 4.14: Mitme nurgaga kujund.
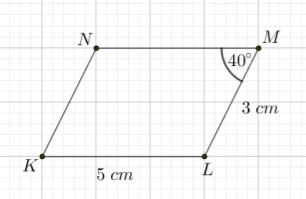
Figure 4.15: Rööpkülik.
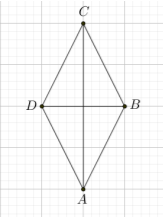
Figure 4.16: Romb.
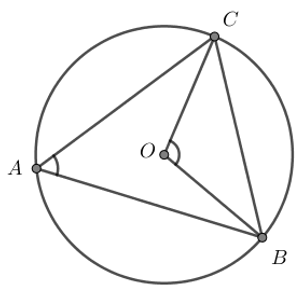
Figure 4.17: Sisenurkadega ring.
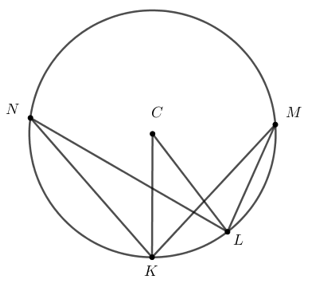
Figure 4.18: Kaks nurka ringjoonelt.
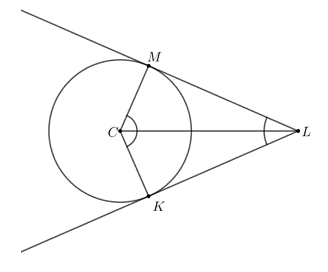
Figure 4.19: Ring puutujatega.
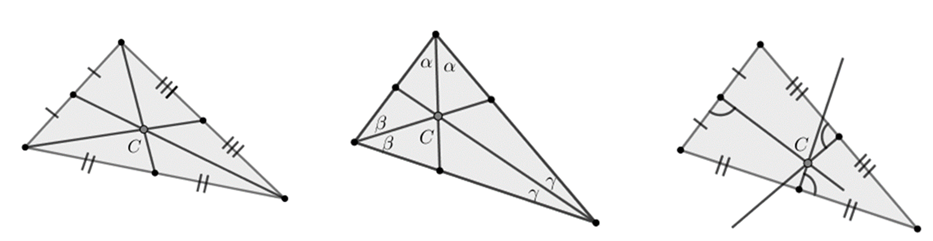
Figure 4.20: Kolmnurgad sisejoontega.
Figure 4.21: Hulknurk.

Figure 4.22: Sarnased kolmnurgad.

Figure 4.23: Kaks sarnast kolmnurka.

Figure 4.24: Maatükk.

Figure 4.25: Kujundi pindala.

Figure 4.26: Graafikud.